¶ Microlensing
作者:黄浩淼 & 刘晓鹏
主分类:Microlensing
¶ 简介:
微引力透镜是由引力透镜效应引起的一种天文现象,可以用来探测从行星质量到恒星质量的物体,允许研究几乎不发光或不发光的物体。它可以研究暗弱天体的数量,如褐矮星、红矮星、行星、白矮星、中子星、黑洞和大质量致密晕天体。用来限制暗物质的性质、探测系外行星、研究遥远恒星的临边昏暗、限制双星星族以及银河系盘的结构。微引力透镜技术也被认为是寻找暗天体,如棕矮星和黑洞,研究恒星黑子,测量恒星自转,探测类星体(包括它们的吸积盘)的一种手段。[1]
¶ 历史背景
1704年,牛顿提出光线可以被重力偏转。1801年,Johann Georg von Soldner计算了牛顿引力下恒星光线的偏转量。1915年,爱因斯坦正确地预测了广义相对论下的偏转量,这是von Soldner预测的两倍。爱因斯坦的预言在1919年由爱丁顿率领的探险队中得到了验证。爱因斯坦于1936年发表了引力透镜产生时源同时变亮的正确预测,成为了微引力透镜的基础。
1979年首次观测到引力透镜现象,是类星体被前景星系引力透镜成像。同年,Kyongae Chang和Sjur Refsdal发现透镜星系中的单个恒星可以在主透镜内充当较小的透镜,导致类星体的图像在几个月的时间尺度上波动,也称为Chang–Refsdal透镜[2]。Bohdan Paczyński首次使用“microlensing”一词来描述这一现象。由于类星体的本身光度会变,这种微引力透镜很难证认,但在1989年,Mike Irwin等人首次发现了微引力透镜[3]。
1986年,Paczyński提出使用微引力透镜,通过观察附近星系中的背景恒星,在银晕中寻找以大质量致密晕天体(MACHO)形式存在的暗物质[4]。两组从事暗物质研究的粒子物理学家听取了他的演讲,并与天文学家共同组成了Anglo-Australian MACHO collaboration和French EROS collaboration。
1986年,Nemiroff, Robert J.预测了微引力透镜的概率[5]。
1991年,Mao和Paczyński提出微引力透镜可以用来寻找恒星的伴星[6],1992年,Gould和Loeb证明微引力透镜可以用于探测系外行星[7]。1992年,Paczyński创立了光学引力透镜实验(Optical Gravitational Lensing Experiment),开始寻找银河系核球方向的事件。1993年,MACHO和EROS在《自然》杂志的背对背论文中报道了可能由暗物质引起的大麦哲伦云方向上的前两次微引力透镜事件,随后几年,这些事件继续被探测到。在这段时间里,Sun Hong Rhie致力于研究系外行星微引力透镜理论,以解释巡天中的事件。MACHO于1999年结束。他们的数据驳斥了100%的暗晕由MACHO组成的假设,但他们发现了大约20%的晕质量过量,这可能是由于MACHO或大麦哲伦星云内部的透镜天体造成的[8]。EROS随后公布了甚至更严格的MACHOs上限[9]。
尽管没有解决暗物质问题,但微引力透镜已被证明是有用工具。每年都会检测到数百次朝向银河系核球的微引力透镜事件,那里的微引力透镜光深(由于银盘中的恒星)大约是穿过银河系晕方向的20倍。2007年,OGLE项目确定了611个事件候选体,MOA项目(一个日本-新西兰合作项目)确定了488个(尽管并非所有候选体都是微引力透镜,而且两个项目之间存在大量重复)。除了以上巡天,后随项目正在进行中,主要目的是探测太阳系外行星,包括MiNDSTEp、RoboNet、MicroFUN和PLANET。
2020年9月,天文学家使用微引力透镜技术首次报告了对一颗地球质量的流浪行星的探测,该行星不受任何恒星的束缚,并在银河系中自由游走[10]。
微引力透镜不仅放大了光源亮度,还移动了它在天球上的表观位置。这一过程的持续时间比亮度放大的持续时间长,可以用来计算透镜的质量。2022年,据报道,这项技术被用于首次明确探测孤立的恒星质量黑洞,利用哈勃太空望远镜长达六年的观测,从2011年8月探测到微引力透镜事件后不久开始。该黑洞的质量约为太阳质量的7倍,距离人马座约1.6千秒差距,而恒星距离人马座则约6千秒差距[11]。我们的星系中有数百万个孤立的黑洞,孤立的黑洞周围几乎没有辐射,因此只能通过微引力透镜来探测。文章的作者们预计,未来的仪器,特别是Nancy Grace Roman Space Telescope和Vera C. Rubin Observatory,将会发现更多的东西。
¶ 物理图像
¶ 基本信息
来自某个源的光线经过某天体附近时,由于引力作用对光线的传播方向会发生偏折,最终使得被观测的天体形状发生改变,这种现象被称为引力透镜效应(如上图)。由于透镜体对光线的偏折,使一部分非视线方向的光线也会被观测到,使得源的辐射流被放大,但同时源平面的面积也会被放大,所以整个过程中平面源的亮度没有发生改变。我们将光子在共动坐标系下的位置标记为,其径向坐标分量等于径向距离χ,横向坐标分量为。其中θ为距离透镜体的横向张角。经过透镜体后,原来处于处的光子被位移到了θ处,所以我们观测到的面源亮度为:
要想获得光子的轨迹和θ之间的关系,我们需要从广义相对论出发,求解光子的测地线方程:



当一颗遥远的恒星或类星体与一个前景物体充分对齐时,由于前景物体引力场,导致光线弯曲,形成两个扭曲的图像(微引力透镜情况下通常无法分辨),从而导致可观察到的亮度增强。瞬时增亮的时间尺度取决于前景对象的质量以及背景“源”和前景“透镜”对象之间的相对自行。
之前的推导需要有广义相对论的基础,对于没有相对论基础的读者可以参考下面的推导:
数学[12]:
当观测者、源和透镜天体处在同一直线上时,光线的偏折角度为:
其中是观测者和透镜的距离,为透镜和源的距离。广义相对论造成光线的偏离为:
得到:
爱因斯坦环角半径:
如果透镜天体偏离观测者和源连线的距离为,则偏离的角距离为。此时两个偏离角度为:
由于透镜保持了表面亮度,每个图像的放大率由图像与光源面积的比率给出,对于“小”光源和任何轴对称透镜,有
则对于一个点质量的透镜,其产生的光度放大为:
其中。此公式有几个重要的性质。(1)总是大于,因此微引力透镜只能增加源星的亮度,而不能降低它。(2)总是随着u的增加而减小,因此对准越近,源星越亮。当接近无穷大时,接近,因此在宽分离时,微引力透镜不起作用。(3)最后,对于点源,当完美对齐()时,理论上是无限的。然而,真实世界的物体不是点源,有限的源尺寸效应将限制非常近的对准光度的放大率,但一些微引力透镜事件可以导致数百倍的亮度。
微引力透镜天体质量较小,也很小因此很难观测到两个像。同时,值改变较快,反应微引力透镜的时标是爱因斯坦时间(Einstein time),是透镜天体走过角距离所花费的时间。是几天至几个月的量级。匀速运动下随着时间的变化为:
如果是点源和点质量透镜天体,则只有是可测量的物理量,其他物理量是互相简并的。而真实的源和透镜是有一定的大小,如果知道源的角半径,可以通过光变曲线估算。同时,透镜天体是双星,具有非线性的运动,也会导致光线曲线发生轻微但可检测的变化,即Xallarap(parallax spelled backwards)效应。爱因斯坦时间较长的微引力透镜事件,由于地球绕太阳转动造成的视差也会产生非线性运动,使得光变曲线与点源和点质量透镜情况下的产生偏离。
¶ 光变曲线

微引力透镜探测系外行星示意图。GIF图来源为Wikipedia[1:1]
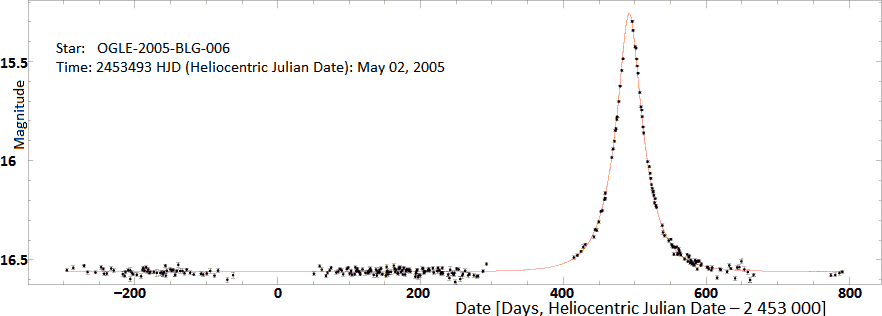
典型的Microlensing光变曲线,光变持续时间可达数百天
¶ 重要文献
[1] Schneider, P. ; Ehlers, J. ; Falco, E. E. Gravitational Lenses. 1992. https://link.springer.com/book/10.1007/978-3-662-03758-4
[2] Gould, A. 2000. A Natural Formalism for Microlensing. The Astrophysical Journal. 542 (2), 785–788.
[3] Paczynski, B. 1986. Gravitational Microlensing by the Galactic Halo. The Astrophysical Journal. 304, p.1.
[4] Alcock, C. ; Allsman, R. A. ; Alves, D. R. et al. 2000. The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations. The Astrophysical Journal, 542 (1), 281-307
[5] Sahu, K. C. ; Anderson, J. ; Casertano, S. et al. 2022. An Isolated Stellar-mass Black Hole Detected through Astrometric Microlensing. The Astrophysical Journal, Volume 933, Issue 1, id.83, 28 pp.
[6] Mao, S. ; Paczynski, B. 1991 Gravitational Microlensing by Double Stars and Planetary Systems. Astrophysical Journal Letters 374, p.L37.
[7] Gould, A. ; Loeb, A. 1992 Discovering Planetary Systems through Gravitational Microlenses Astrophysical Journal 396, p.104.
[8] Einstein, A. 1936 Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field.* Science*, 84, 2188, 506-507
[9] Joachim Wambsganss 2006 Gravitational Lensing: Strong, Weak and Micro. https://link.springer.com/book/10.1007/978-3-540-30310-7
[10] Alcock C. et al. The MACHO project: Microlensing Optical Depth towards the Galactic Bulge from Difference Image Analysis. The Astrophysical Journal. 541 (2): 734–766.
¶ 参考文献
https://en.wikipedia.org/wiki/Gravitational_microlensing ↩︎ ↩︎
Chang, K.; Refsdal, S. 1979. Flux variations of QSO 0957 + 561 A, B and image splitting by stars near the light path. Nature. 282 (5739): 561–564. ↩︎
Mike I.; et al. 1989. Photometric Variations in the Q2237+0305 System: First Detection of a Microlensing Event. The Astronomical Journal. 98: 1989. ↩︎
Paczynski, B. 1986 Gravitational Microlensing by the Galactic Halo. The Astrophysical Journal. 304, p.1. ↩︎
Nemiroff, R. J. 1986. Random gravitational lensing. Astrophysics and Space Science. 123 (2): 381–387. ↩︎
Mao, S. ; Paczynski, B. 1991. Gravitational Microlensing by Double Stars and Planetary Systems. Astrophysical Journal Letters 374, p.L37. ↩︎
Gould, A. ; Loeb, A. 1992. Discovering Planetary Systems through Gravitational Microlenses Astrophysical Journal 396, p.104. ↩︎
Alcock, C. ; Allsman, R. A. ; Alves, D. R. et al. 2000. The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations. The Astrophysical Journal, 542 (1), 281-307 ↩︎
Tisserand, P.; Le Guillou, L.; Afonso, C. et al. 2007. Limits on the Macho content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds. Astronomy and Astrophysics. 469 (2): 387–404. ↩︎
Mroz, Przemek; et al. 2020. A terrestrial-mass rogue planet candidate detected in the shortest-timescale microlensing event. The Astrophysical Journal. 903 (1): L11. ↩︎
Sahu, K. C. ; Anderson, J. ; Casertano, S. et al. 2022. An Isolated Stellar-mass Black Hole Detected through Astrometric Microlensing. The Astrophysical Journal, Volume 933, Issue 1, id.83, 28 pp. ↩︎
Gould, A. 2000. A Natural Formalism for Microlensing. The Astrophysical Journal. 542 (2), 785–788. ↩︎