¶ Doradus
作者:韩恒赓
主分类:脉动变星
¶ 历史背景
早在1963年,Cousins & Warren (1963)变发现了一颗名为 Doradus的变星[1]。该恒星的光变曲线可由多个周期差别很小的正余弦模型共同描述。其中两个最为显著的周期为:0.733与0.757天。该恒星的绝对亮度与典型的 Scuti变星的绝对亮度相似,但是却有着更低的温度。故而早些时候该恒星的光变机制一直不明朗。
起初人们尝试用两个黑子结合较差自转来描述该恒星的光变[2]。然而为了造成如此大的振幅,需要较大的黑子。同时考虑到恒星的光变周期极其稳定,故而这类解释显然是不成立的。另外,该变星的过长的光变周期使得我们无法将其归为p-模震荡的 Scuti类星震变星。各类证据都指向了存在另一类变星这一结论。
随着观测的增多,越来越多的典型恒星被发现,其中包括:(1)HD 164615[3];(2)9 Aur[4];(3)HD 111828[5];(4)HD 224638[6];(5)HD 224945[7]。受限于观测手段与样本数量,起初人们无法揭示这些恒星光变的本源。直至二十世纪末期时,随着数据的进一步积累,该类变星先后被Balona et al.(1994)[2:1]与Kaye et al.(1999)[8]认证为一类新的星震变星分支,即为 Dor星震变星,其光变曲线的周期性变化与振幅的准周期性变化来自于g-模的非径向震动。
新一代望远镜的出现,提供了海量的光变曲线数据并极大补充了 Dor的数据库。例如Balona et al. (2011)[9]给出了开普勒视场内10000颗A-F型恒星的的统计样本,并发现其中1/3的恒星处在赫罗图中 Dor类变星所在的区域。Bradley et al. (2015)[10]搜寻到了207颗 Dor。这些大样本数据酷极大的丰富了人们对 Dor变星的认识并为研究其物理图像提供了夯实的数据基础。
¶ 物理图像
¶ 演化阶段
Dor在赫罗图的位置如图1所示。位于主序之上的很窄的一片区域,主要由F型恒星与晚型的A型恒星构成,且与温度较低的 Scuti变星有一定的交叠。
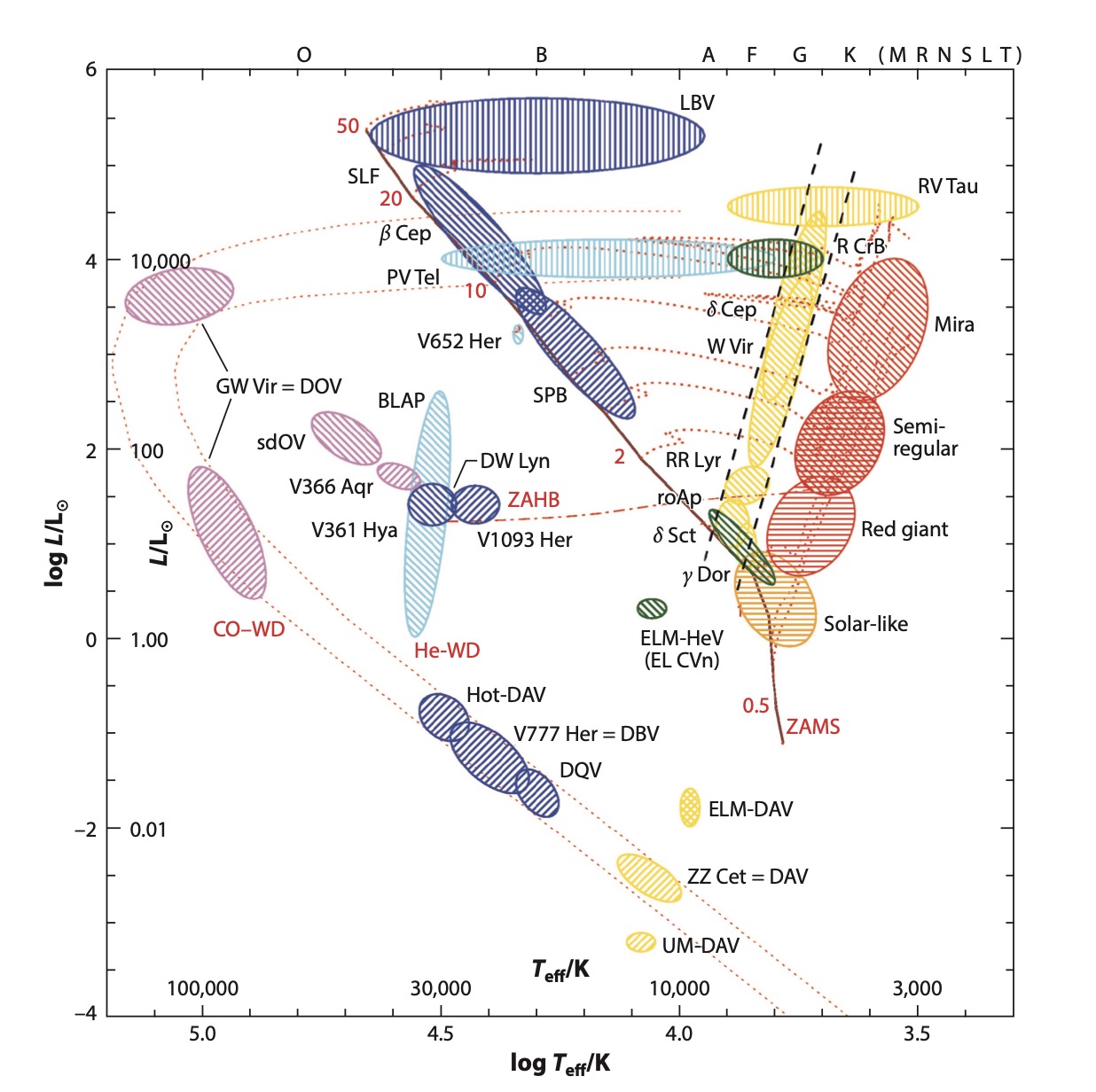
图1.各类脉动变星在赫罗图上的区域分布图。图片来源:Kurtz. 2022[11]
¶ 脉动机制
位于图1中绿色椭圆区域内的恒星,由部分电离的氦原子和氢原子构成的较薄的对流区域会逐渐合并并形成较大的对流包层。这些对流包层的底部阻挡并吸收了部分来自恒星内部的热辐射。之后为了达到热平衡,这些区域便需要向外扩张,从而释放部分能量。之后物质收缩,并继续阻挡并吸收来自恒星内部的热辐射。该过程被命名为:convective blocking[12],即 Dor类变星的震动机制。 Dor的震动模式为g-模震动,典型震动周期在0.3-3天。
¶ 光变曲线及其性质
¶ 光变曲线
在图2中我们给出了一颗典型的 Dor变星,KIC 4547348的部分光变曲线。其中横坐标为开普勒望远镜的观测时间,纵坐标为归一化流量。
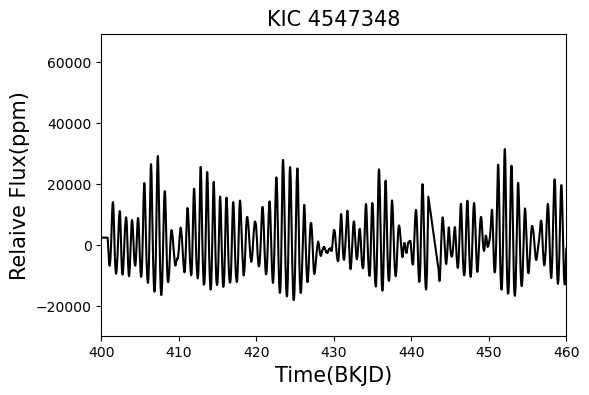
图2.KIC 4547348的光变曲线。
可以看出,光变曲线主要表现出两个特征:(1)类似正余弦的准周期调制。(2)光变曲线振幅表现出准周期性变化。通常来说,很难区分 Dor变星的光变曲线与恒星黑子对应的光变曲线。 Dor类变星的光变曲线通常表现出两类特征:(1)较为对称的“拍”结构。(2)较为不对称的“拍”结构。若对应了前者, Dor样本则很有可能被磁活动恒星所污染。
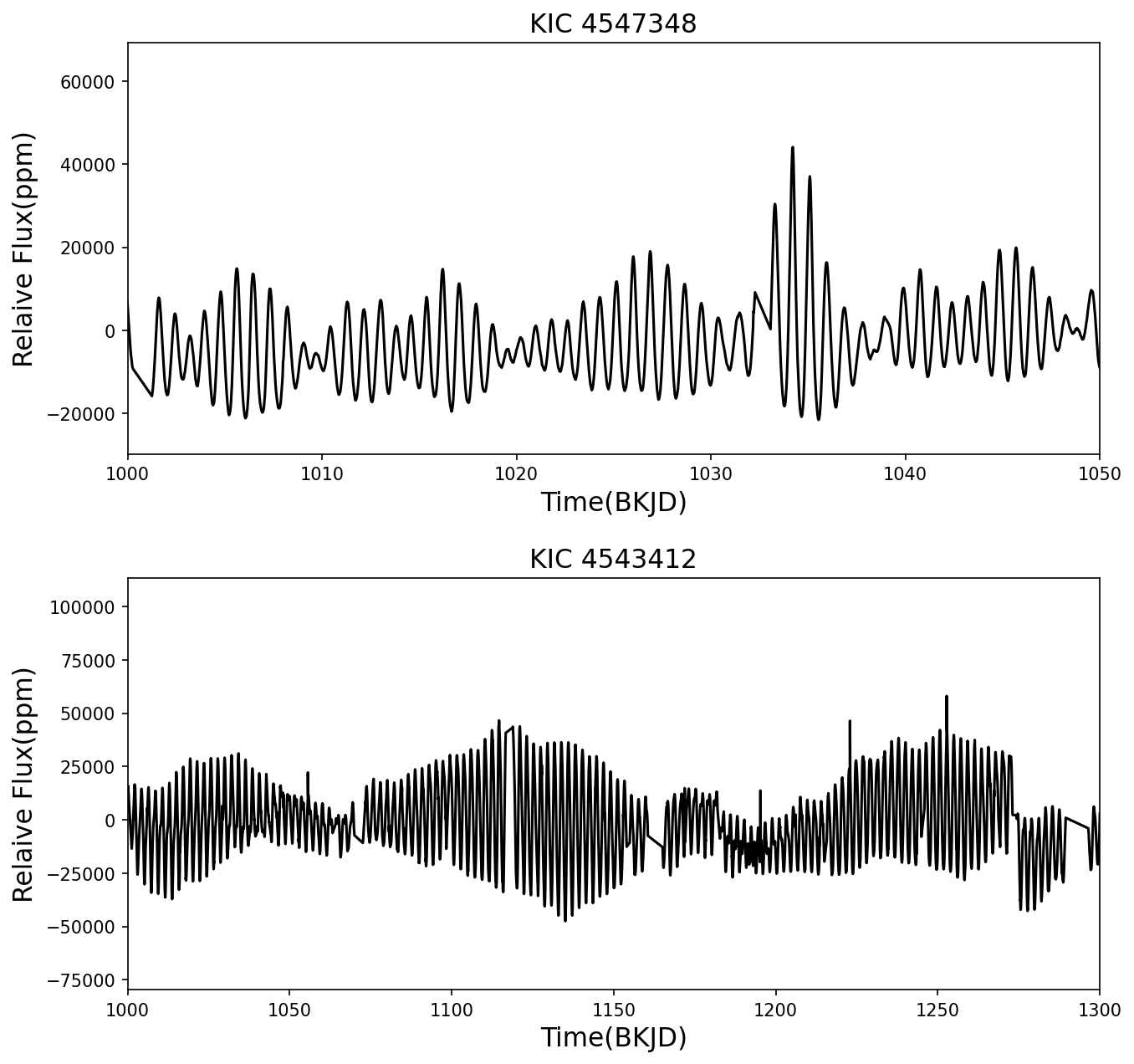
图3.自转变星KIC 4543412与 Dor变星KIC 4547348的光变曲线的对比图。
如图3所示,我们给出了两颗恒星的光变曲线的对比图。其中KIC 4543412为自转变星,而KIC 4547348为 Dor变星。可以看出,虽然时标有所不同,但是两者的光变曲线具有较高的相似性。故而很难清晰的区分两者。不过通常来说, Dor类变星的光变曲线的类似正余弦的调制的形状较为稳定。自转变星所对应的正余弦调制的形状,包括左右不对称性,往往会随着时间的变化而变化,从而使得光变曲线的频谱图中主频的各级谐频发生变化。同时,光变曲线的振幅极小值处若表现较为稳定的”双峰“结构,则有很有可能对应了黑子造成的光变。
¶ 频谱图
在图4中我们给出了KIC 4547348的光变曲线的频谱图。
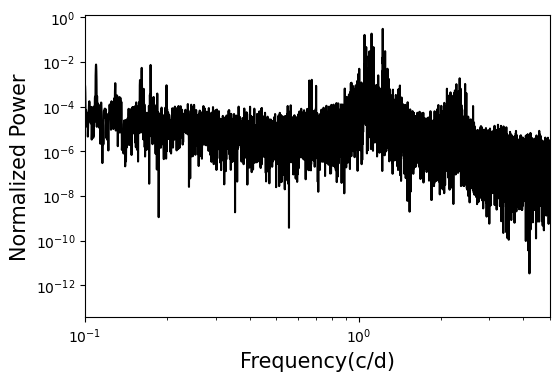
图4.KIC 4547348的光变曲线的频谱图。
可以明显看出,在频谱中大约1.2(c/d)处出现了一个频率簇。其中最显著的峰值显然对应了光变曲线中的类似正余弦的调制。而其它相近的频率则对应了光变曲线振幅的较为不规律的准周期变化。而约2.4(c/d)频率处的峰值则是二倍频。
¶ 二维相位折叠图

图5.KIC 4547348的光变曲线的二维相位折叠图。横坐标代表了观测时间,纵坐标代表了震动相位,颜色代表了光变曲线的归一化振幅。
在图5中我们给出了该源的光变曲线的二维相位折叠图。可以看出,光变曲线的形状(相位)保持的相当稳定。
¶ 短时傅里叶变换图
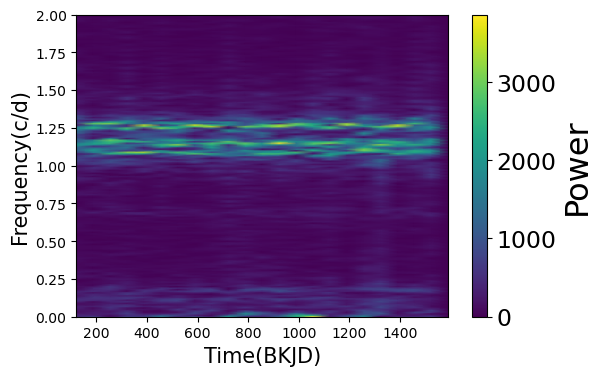
图6.KIC 45473484的光变曲线的短时傅立叶变换图。横坐标代表观测时间,纵坐标代表光变曲线的频率成分,颜色代表了频率所对应的功率大小。
在图6中我们给出了KIC 45473484的短时傅立叶变换图。其中横坐标为观测时间,纵坐标为频率,颜色代表了频率的强度。显然的,在1.2(c/d)的频率附近出现了频率簇。且该频率簇在开普勒的观测时长内保持了较为稳定的状态。图中同样可以看出,随着时间的变化,频率簇内的某些频率成分的强度表现出了一定程度的变化。
¶ 恒星光谱
在图7中我们给出了KIC 4547348的LAMOST光谱。
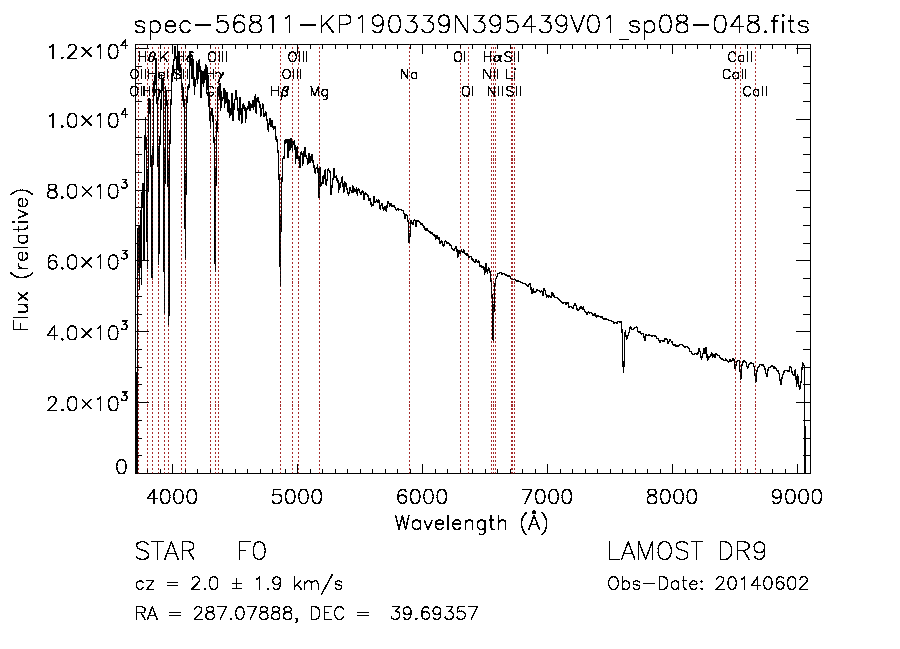
图7.KIC 45473484的LAMOST光谱。
¶ 参考文献
Cousins A. W. J., Warren P. R., 1963, Mon. Notes Astron. Soc. South. Africa, 22, 65 ↩︎
Balona, L.~A., Krisciunas, K., & Cousins, A.W.J. 1994, mnras, 270, 905. ↩︎ ↩︎
Burke, E.~W., Burke, E.~W., & Lady, S. 1977, Information Bulletin on Variable Stars, 1279, 1 ↩︎
Krisciunas, K. & Guinan, E.1990, Information Bulletin on Variable Stars, 3511, 1 ↩︎
Mantegazza, L., Poretti, E., & Antonello, E. 1991, Information Bulletin on Variable Stars, 3612, 1 ↩︎
Mantegazza, L. & Poretti, E. 1991, Information Bulletin on Variable Stars, 3690, 1 ↩︎
Mantegazza, L., Poretti, E., & Zerbi, F.~M. 1994, Delta Scuti Star Newsletter, Issue 7, p. 4-4., 7 ↩︎
Kaye, A.~B., Handler, G., Krisciunas, K., et al. 1999, pasp, 111, 840. doi:10.1086/316399 ↩︎
Balona, L.~A., Guzik, J.~A., Uytterhoeven, K., et al. 2011, mnras, 415, 3531. doi:10.1111/j.1365-2966.2011.18973.x ↩︎
Bradley, P.~A., Guzik, J.~A., Miles, L.~F., et al. 2015, aj, 149, 68. doi:10.1088/0004-6256/149/2/68 ↩︎